第五章：通过组合进行编码

函数式的组合培育

这是 compose 函数：

const compose = (...fns) => (...args) => fns.reduceRight((res, fn) => [fn.call(null, ...res)], args)[0];

... 别害怕！这是 compose 的究极超级赛亚人形态。为了便于理解，让我们暂时放下这个可变参数（variadic）的实现，考虑一个更简单的形式，它可以组合两个函数。一旦你理解了那个，你就可以进一步推广这个抽象，并认为它适用于任意数量的函数（我们甚至可以证明这一点）！ 亲爱的读者们，这里有一个更友好的 compose：

const compose2 = (f, g) => x => f(g(x));

f 和 g 是函数，x 是通过它们“流经”的值。

组合感觉就像函数的培育。你，作为函数的培育者，选择两个具有你想要结合的特性的函数，并将它们混合在一起，生成一个全新的函数。用法如下：

const toUpperCase = x => x.toUpperCase(); // 转为大写
const exclaim = x => `${x}!`; // 添加感叹号
const shout = compose(exclaim, toUpperCase); // 先 toUpperCase，然后 exclaim

shout('send in the clowns'); // "SEND IN THE CLOWNS!"

两个函数的组合返回一个新函数。这完全合乎逻辑：组合某个类型的两个单元（这里是函数）应该产生一个相同类型的新单元。你不会把两个乐高（legos）积木拼在一起得到一个林肯积木（Lincoln Log）。这里存在一种理论，一些潜在的规律，我们将在适当的时候发现它。

在我们的 compose 定义中，g 会在 f 之前运行，创建了一个从右到左的数据流。这比嵌套一堆函数调用更具可读性。没有 compose，上面的代码会是这样：

const shout = x => exclaim(toUpperCase(x));

我们不是从内到外执行，而是从右到左执行，我想这是朝着“左”的方向迈出一步（嘘！）。让我们看一个顺序很重要的例子：

const head = x => x[0]; // 获取第一个元素
const reverse = reduce((acc, x) => [x, ...acc], []); // 反转数组
const last = compose(head, reverse); // 先 reverse，然后 head

last(['jumpkick', 'roundhouse', 'uppercut']); // 'uppercut'

reverse 会将列表反转，而 head 则获取第一个元素。这产生了一个有效但效率不高的 last 函数。组合中函数的顺序在这里应该很明显。我们可以定义一个从左到右的版本，然而，目前这样更贴近数学上的版本。没错，组合直接源自数学课本。事实上，也许是时候看看对于任何组合都成立的一个属性了。

// 结合律 (associativity)
compose(f, compose(g, h)) === compose(compose(f, g), h);

组合是满足结合律的，这意味着你如何对它们进行分组并不重要。所以，如果我们选择将字符串转换为大写，我们可以写：

compose(toUpperCase, compose(head, reverse));
// 或者
compose(compose(toUpperCase, head), reverse);

因为我们如何对 compose 调用进行分组并不重要，结果将是相同的。这允许我们编写一个可变参数的 compose 并像下面这样使用它：

// 以前我们必须写两个 compose 调用，但由于它是结合律的，
// 我们可以给 compose 任意数量的函数，让它决定如何分组。
const arg = ['jumpkick', 'roundhouse', 'uppercut'];
const lastUpper = compose(toUpperCase, head, reverse); // 从右到左执行：reverse, head, toUpperCase
const loudLastUpper = compose(exclaim, toUpperCase, head, reverse); // 从右到左执行：reverse, head, toUpperCase, exclaim

lastUpper(arg); // 'UPPERCUT'
loudLastUpper(arg); // 'UPPERCUT!'

应用结合律属性给了我们这种灵活性，并让我们安心，结果将是等价的。稍微复杂一点的可变参数定义包含在本书的支持库中，并且是你在 lodash、underscore 和 ramda 等库中会找到的标准定义。

结合律的一个令人愉快的好处是，任何一组函数都可以被提取出来并捆绑在它们自己的组合中。让我们来重构一下之前的例子：

const loudLastUpper = compose(exclaim, toUpperCase, head, reverse);

// -- 或者 ---------------------------------------------------------------

const last = compose(head, reverse);
const loudLastUpper = compose(exclaim, toUpperCase, last);

// -- 或者 ---------------------------------------------------------------

const last = compose(head, reverse);
const angry = compose(exclaim, toUpperCase);
const loudLastUpper = compose(angry, last);

// 更多变种...

没有正确或错误的答案——我们只是以任何我们喜欢的方式将我们的乐高积木拼在一起。通常最好将事物以可复用（reusable）的方式分组，比如 last 和 angry。如果熟悉福勒（Fowler）的《重构》，可能会认出这个过程是“提取函数”……只是没有那么多对象状态需要担心。

Pointfree

Pointfree 风格意味着永远不必提及你的数据。不好意思，说错了。它指的是函数从不提及它们操作的数据。一等函数、柯里化和组合都很好地协同工作来创建这种风格。

提示：replace 和 toLowerCase 的 Pointfree 版本定义在附录 C - Pointfree 工具函数中。不要犹豫，去看看吧！

// 不是 pointfree，因为我们提到了数据：word
const snakeCase = word => word.toLowerCase().replace(/\s+/ig, '_');

// pointfree
const snakeCase = compose(replace(/\s+/ig, '_'), toLowerCase);

看到我们如何部分应用（partially applied）replace 了吗？我们正在做的是将我们的数据通过管道传递给每个只接收 1 个参数的函数。柯里化允许我们准备好每个函数，让它们只接收数据，对其进行操作，然后传递下去。另一件值得注意的事情是，在 pointfree 版本中，我们不需要数据来构造我们的函数，而在有参数（pointful）的版本中，我们必须先有 word 才能做任何事情。

让我们看另一个例子。

// 不是 pointfree，因为我们提到了数据：name
const initials = name => name.split(' ').map(compose(toUpperCase, head)).join('. ');

// pointfree
// 注意：我们使用了附录中的 'intercalate' 而不是第九章介绍的 'join'！
const initials = compose(intercalate('. '), map(compose(toUpperCase, head)), split(' '));

initials('hunter stockton thompson'); // 'H. S. T'

Pointfree 代码可以再次帮助我们移除不必要的名称，并保持代码简洁和通用。Pointfree 是函数式代码的一个很好的试金石，因为它让我们知道我们拥有的是接收输入并产生输出的小函数。例如，人们无法组合一个 while 循环。但请注意，pointfree 是一把双刃剑，有时会混淆意图。并非所有函数式代码都是 pointfree 的，这没关系。我们尽可能争取使用它，否则就坚持使用普通函数。

调试

一个常见的错误是在没有先部分应用的情况下组合像 map 这样的双参数函数。

// 错误 - 我们最终把一个数组传给了 angry，并且天知道我们用什么部分应用了 map。
const latin = compose(map, angry, reverse);

latin(['frog', 'eyes']); // error

// 正确 - 每个函数都期望接收 1 个参数。
const latin = compose(map(angry), reverse);

latin(['frog', 'eyes']); // ['EYES!', 'FROG!'])

如果你在调试组合时遇到困难，我们可以使用这个有用但非纯的 trace 函数来看看发生了什么。

const trace = curry((tag, x) => {
  console.log(tag, x); // 打印标签和当前值
  return x; // 返回原始值
});

const dasherize = compose(
  intercalate('-'),
  toLower,
  split(' '),
  replace(/\s{2,}/ig, ' '),
);

dasherize('The world is a vampire');
// TypeError: Cannot read property 'apply' of undefined (类型错误：无法读取未定义的属性 'apply')

这里有些问题，让我们用 trace 追踪一下。

const dasherize = compose(
  intercalate('-'),
  toLower,
  trace('after split'), // 在 split 之后追踪
  split(' '),
  replace(/\s{2,}/ig, ' '),
);

dasherize('The world is a vampire');
// after split [ 'The', 'world', 'is', 'a', 'vampire' ] // split 后的结果

啊哈！我们需要对这个 toLower 进行 map 操作，因为它作用于一个数组。

const dasherize = compose(
  intercalate('-'),
  map(toLower), // 对数组中的每个元素应用 toLower
  split(' '),
  replace(/\s{2,}/ig, ' '),
);

dasherize('The world is a vampire'); // 'the-world-is-a-vampire'

trace 函数允许我们为了调试目的查看特定点的数据。像 Haskell 和 PureScript 这样的语言也有类似的函数，以方便开发。

组合将是我们构建程序的工具，而且幸运的是，它由一个强大的理论支撑，确保事情会顺利进行。让我们来研究一下这个理论。

范畴论

范畴论（Category Theory）是数学的一个抽象分支，它可以形式化来自几个不同分支的概念，如集合论（set theory）、类型论（type theory）、群论（group theory）、逻辑学（logic）等等。它主要处理对象（objects）、态射（morphisms）和变换（transformations），这与编程非常相似。这是一个从各种不同理论视角看待相同概念的图表。

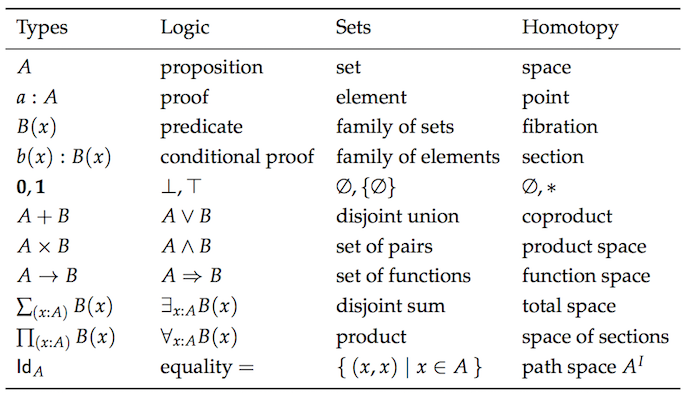
范畴论概念图

抱歉，我不是故意吓唬你。我不期望你对所有这些概念都了如指掌。我的观点是向你展示我们有多少重复的东西，这样你就能明白为什么范畴论旨在统一这些事物。

在范畴论中，我们有一个叫做……范畴（category）的东西。它被定义为一个具有以下组件的集合：

  • 一个对象的集合
  • 一个态射的集合
  • 态射上的组合概念
  • 一个称为同一性（identity）的特殊态射

范畴论足够抽象，可以模拟许多事物，但让我们将其应用于类型和函数，这是我们目前关心的。

一个对象的集合 对象将是数据类型。例如，String、Boolean、Number、Object 等。我们经常将数据类型视为所有可能值的集合。可以把 Boolean 看作是 [true, false] 的集合，把 Number 看作是所有可能数值的集合。将类型视为集合很有用，因为我们可以使用集合论来处理它们。

一个态射的集合 态射将是我们日常使用的标准纯函数。

态射上的组合概念 你可能已经猜到了，这就是我们的新玩具——compose。我们已经讨论过我们的 compose 函数满足结合律，这并非巧合，因为这是范畴论中任何组合都必须满足的属性。

这是一张演示组合的图片：

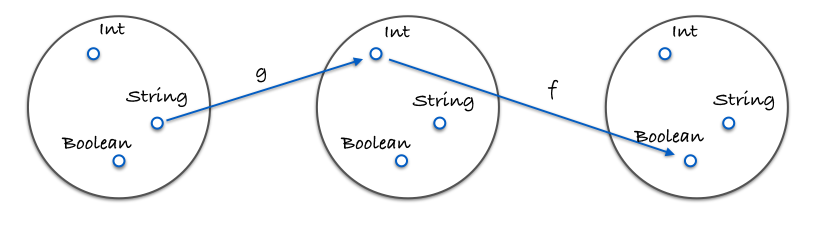
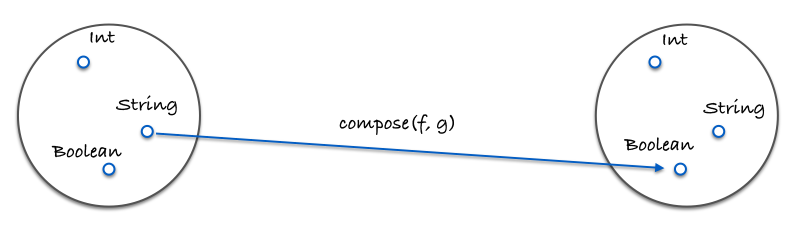
范畴组合 1 范畴组合 2

这是一个代码中的具体例子：

const g = x => x.length; // 态射 g：输入 x，输出 x.length
const f = x => x === 4; // 态射 f：输入 x，输出 x 是否等于 4
// isFourLetterWord 是 f 和 g 的组合 (f . g)
const isFourLetterWord = compose(f, g);

一个称为同一性（identity）的特殊态射 让我们介绍一个有用的函数叫做 id。这个函数只是接收一些输入，然后原封不动地把它吐出来。看一下：

const id = x => x;

你可能会问自己“这到底有什么用？”。在接下来的章节中，我们将广泛使用这个函数，但现在你可以把它看作是一个可以代表我们值的函数——一个伪装成日常数据的函数。

id 必须与 compose 良好协作。对于每个一元函数（unary: 一个参数的函数）f，以下属性始终成立：

// 同一性 (identity)
compose(id, f) === compose(f, id) === f;
// true

嘿，这就像数字上的单位元属性！如果这不是很明显，花点时间思考一下。体会它的精妙之处。我们很快就会看到 id 被到处使用，但现在我们看到它是一个充当给定值的替身的函数。这在编写 pointfree 代码时非常有用。

所以，这就是类型和函数的范畴。如果这是你第一次接触，我想你对范畴是什么以及它为什么有用仍然有点模糊。我们将在整本书中建立在这方面的知识之上。就目前而言，在本章中，在这一行，你至少可以看到它为我们提供了一些关于组合的智慧——即结合律和同一性属性。

你问还有哪些其他的范畴？嗯，我们可以为有向图定义一个范畴，其中节点是对象，边是态射，而组合就是路径连接。我们可以定义一个以数字为对象，>= 为态射的范畴（实际上任何偏序（partial order）或全序（total order）都可以是一个范畴）。有大量的范畴，但为了本书的目的，我们只关心上面定义的那个。我们已经充分地浅尝辄止，必须继续前进了。

总结

组合像一系列管道一样将我们的函数连接在一起。数据将必须流经我们的应用程序——毕竟纯函数是输入到输出的，所以打破这个链条将忽略输出，使我们的软件毫无用处。

我们将组合视为高于一切的设计原则。这是因为它使我们的应用程序保持简单且易于理解。范畴论将在应用程序架构、建模副作用和确保正确性方面发挥重要作用。

我们现在到了一个节点，看到一些实际应用会对我们很有帮助。让我们来做一个示例应用程序。

第六章：示例应用程序

练习

在下面的每个练习中，我们将考虑具有以下结构的 Car 对象：

{
  name: 'Aston Martin One-77', // 名称
  horsepower: 750, // 马力
  dollar_value: 1850000, // 美元价值
  in_stock: true, // 是否有库存
}

Exercise
Correct!
False!
使用 `compose()` 重写下面的函数。
// isLastInStock :: [Car] -> Boolean const isLastInStock = (cars) => { const lastCar = last(cars); return prop('in_stock', lastCar); };
Submit Solution

考虑以下函数：

// 计算平均值
const average = xs => reduce(add, 0, xs) / xs.length;

Exercise
Correct!
False!
使用辅助函数 `average` 将 `averageDollarValue` 重构为一个组合。
// averageDollarValue :: [Car] -> Int const averageDollarValue = (cars) => { const dollarValues = map(c => c.dollar_value, cars); return average(dollarValues); };
Submit Solution

Exercise
Correct!
False!
使用 `compose()` 和其他函数以 pointfree 风格重构 `fastestCar`。提示， `append` 函数可能会派上用场。
const fastestCar = (cars) => { const sorted = sortBy(car => car.horsepower, cars); const fastest = last(sorted); return concat(fastest.name, ' is the fastest'); };
Submit Solution

results matching ""

    No results matching ""